

HYB is an open source hybrid code for space plasma simulations (see GitHub/HYB and HWA). Hybrid codes are powerful tools to model plasma interactions of celestial bodies. In the hybrid approach ions are treated as particles while electrons are a fluid. The advantage of a hybrid model is that the ion velocity distributions need not be prescribed in advance as they evolve self-consistently in the model while leaving out electron kinetics, which are computationally expensive. Hybrid models are by definition of multifluid nature: they are able to solve plasma interactions of ion populations with different particle charges and masses.
These features of the HYB code are useful for plasma interactions of planets, moons and comets since ionospheric and solar wind and co-rotating magnetospheric plasmas consist of several ion species and ion finite Larmor radius (FLR) effects can play an important role.
Quasi-Neutral Hybrid model
Solving the model
Numerical methods
The HYB simulation is based on the quasi-neutral hybrid (QNH) description of plasma. In the QNH model positively charged ions are treated explicitly as kinetic particles moving under the Lorentz force in electric and magnetic field. Electrons are modelled as a charge-neutralizing and massless fuid. The ions are self-consistently coupled to the electric field and the magnetic field via the ion charge density and the ion current density, which are the source terms in the non-radiative Maxwell equations. Physical laws of the QNH model are the following.

Dynamics of the ions in the electric and magnetic field are governed by the Lorentz force and Newton's second law (i = single ion):
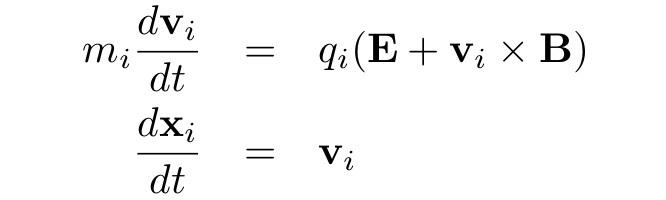
Electrons are considered implicitly as an inertialess fluid by the fluid momentum equation (Ohm's law):
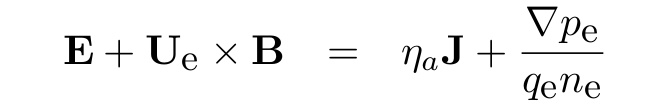
Ideal gas law is used as the electron equation of state:
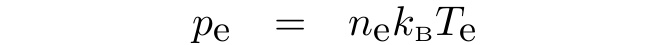
Quasi-neutrality condition of the plasma is (i = sum over all ions in a grid cell):
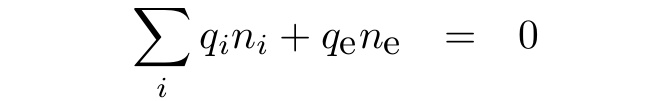
Electric current density is defined as:
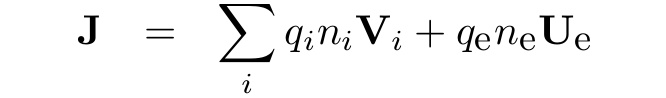
Electrodynamics follow from the non-radiative Maxwell equations:
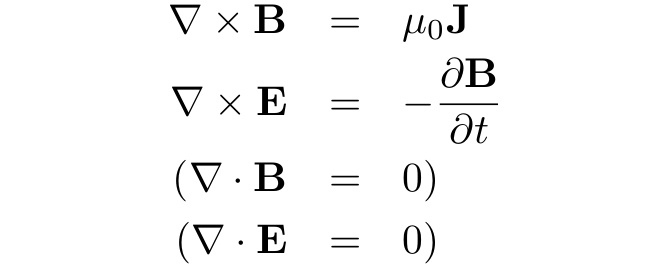
The equations of the QNH model are solved by starting with known initial values for the ions (positions and velocities) and the magnetic field.
Time loop of the solver advances as follows:
1. Current density is obtained from the magnetic field via Ampère's law:

2. Electron charge density in a grid cell comes from the quasi-neutrality assumption:
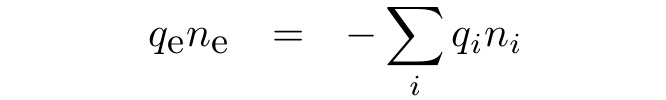
3. Electron velocity is determined from the definition of the total current density:
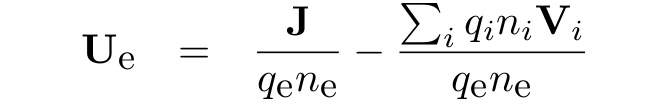
4. Electric field is calculated from the electron momentum equation and the ideal gas law as the electron equation of state assuming here isothermal electrons (Te = const.):
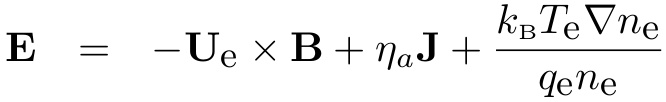
5. Magnetic field is advanced by Faraday's law:
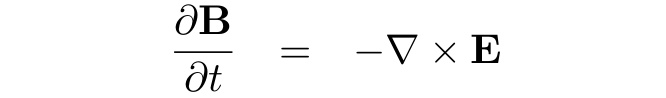
6. Ions are accelerated by the Lorentz force and moved by Newton's second law:
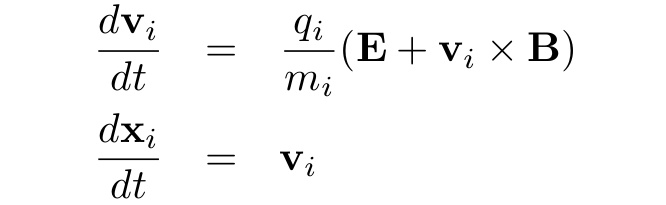
The HYB code uses the Yee type staggered grid (a spatial simulation mesh) to store the magnetic field on grid cell faces. The electric field is evaluated on grid cell nodes or grid cell edges, which guarantees that the divergence of the magnetic field remains zero. Cartesian or spherical coordinate system can be used. The mesh is hierarchically refinable allowing increased spatial resolution where it is needed within the simulation domain.
Positively charged ions are modelled as particle clouds moving in the HYB simulation domain (Cloud-In-Cell technique). Each particle cloud (macroparticle) represents a number of real physical ions described by the statistical weight factor. Particles are accumulated in the mesh to determine the ion charge density and the ion current density (the ion moments). In the ion accumulation the weight factor and the cloud shape (e.g. trilinear) are used to evaluate how many physical particles in the cloud belong to each grid cell the cloud overlaps with.
Macroparticle splitting and joining allows the control over the average number of computational ions in the HYB simulation. Ions can be joined (3->2) if too many macroparticles are found in a grid cell. And ions can be splitted (1->2) if too few macroparticles are found in a grid cell. The conservations laws are satisfied in the particle splitting and joining. This technique is needed when using several leves of grid refinements to allow enough (but not too many) macroparticles to be modelled in the simulation.
Details on the numerical algorithm of the HYB code can be found here: doi:10.5194/angeo-21-2133-2003. The spherical version of HYB is described here: doi:10.1002/jgra.50497. More details of the numerical implementation of HYB can be found in the following PhD theses: ISBN: 978-951-697-660-3 and ISBN: 978-951-697-740-2.